2018年〜2019年にかけて数学検定1級対策というワードで検索順位1位を獲得し、
多くの数学検定1級受験者にお読みいただいた記事を全面リニュアールしたものを最新の情報を加えてお届けします。
2023年以降の数学検定1級に合格するための方法を、70回分を超える過去問をもとに分析し、合格するための方法を1から教えます。
数学検定1級の難易度と数検1級取得のメリット
数学検定1級のレベルは大学程度の難易度です。
高校数学範囲の問題では東大の過去問とそっくりな問題などが散見されるため、大学入試では最高難度の数学力が求められます。
例えば東大数学2005年の第6問の直交3円柱の体積の問題がほぼそのまま出ています。
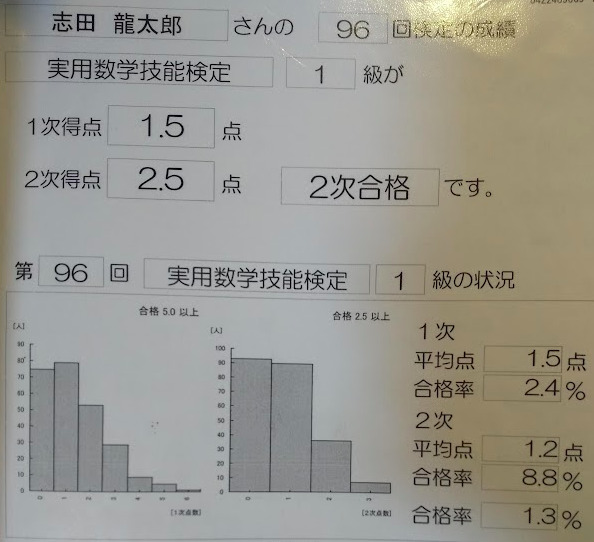
合格率は近年では5~10%程度となっています。他の検定の1級と比べて合格率1%回などもある受験回によって難易度がぶれる試験です。
数学検定1級の歴史は古く、最も低い回が1.3%です。(ちょうど僕が当たってしまった回です)
ただし毎回1%だとほとんど誰も合格できないので、協会側の難易度設定に苦心している様子が伺えます。
数学検定1級は大学程度と言っていましたが、具体的にはどのあたりなのでしょうか。
まず大学のレベルは平均的な理工系大学と思ってOKです。大学の学年のレベルは2年生までに習う範囲が出題の中心になります。
数学検定1級の難易度について、数学検定のサイトでは難易度表示が変わった時が複数ありました。
大学初年度程度
大学卒業程度
大学程度
このような流れで難易度表示が変化してきました。ここから数学検定協会の1級に対する考え方の変化が見て取れます。
現在の数学検定1級の立ち位置は理工系大学の数学的処理ができるレベルとなります。そして大学院入試数学の基準をクリアするための前段階という難易度になります。
実際に東大院試を突破したので説得力がありますね!
純粋数学でよく用いるε-δ論法やルベーグ積分などは全く出ないのでご安心ください!
数学検定1級は時間制限的な難しさもあります!1次試験の時間の足りなさを克服するのが難しい試験です。
1次は60分で問題を7問解く→答えのみが要求されて5問以上で合格。
2次は120分で問題を7問与えられ、2問は必須で残りは5問中2問選択する。→すべて記述方式で合計で2.5問以上で合格となる。
僕が合格した2005年頃は1次の方が2次より難しかったのですが、現在では2次の難易度が上がってきています。
しかし数学検定1級の2次試験の応用数学部分は表面的な問題がほとんどですので演習量が大切です。
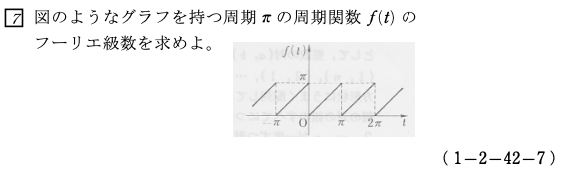
大学院入試ではこれ以上の理解が問われますが、数学検定1級では表面的な計算でおしまいです。
さらに実は統計の問題が得意だと確実に1問完答できます。ある意味で裏技かも知れません。
『マセマ』シリーズはとてもおすすめで中学生の頃の僕でも読めたので、わかりやすくおすすめです。
現在、統計検定1級の勉強をしている身としても、本格的なわかりやすい入門書として素晴らしい本だと思っています。
もちろん本書の内容が頭に入れば、数学検定1級の2次の統計問題の多くは解けるようになります。
上であったフーリエ解析の本もありますので、是非とも探しに行ってみてください!
反対に1次の問題はテンプレ問題が増えてしまったため、過去問での対策が必須になります。
数学検定1級1次の歴代最難問を教えてください。
第96回検定(2004/11)の問題7ですね。

このような形の偏微分方程式をノーヒントで解かせる問題はこの問題を最後に1度も出ていません。
しかもこれは答えのみなので相当正解するのが厳しい問題です。
実際はこの問題以外にも強烈な極限問題もあり、
やはり第96回は歴代最難関の回でした。
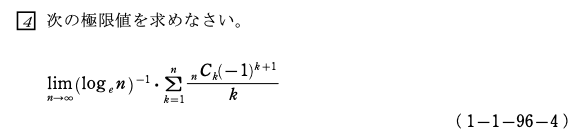
しかし、こういう問題はイレギュラーであり、現在の1次は毎回似たようなパターンばかりになってしまったため、対策はしやすいと思います!
まとめると現在の数学検定1級の難易度は次のようにまとめられます。
1次はパターンで合格点が取れる。
2次は実力勝負である。
数学検定1級は2次の突破力が本質となる。
数学検定1級の参考書と過去問に対する考え方

参考書はインプット
過去問はアウトプット
まずはこの考えが基本です。
合格するために参考書を買おうと思います。でもどれを買ったら良いのかわかりません!
過去問をゲットするつもりで参考書を購入する観点が良いと思います!
2012年以降に数学検定協会は参考書を出し始めました。それ以降で問題の難易度はかつてほどの振れ幅はなく、一定になってきた感じを受けます。
2次の難易度が上昇していることと
1次の対策がしやすくなったこと
この2つを念頭において解説していきます。
以前の改訂前の記事では時系列順に紹介していました。
そして合格を優先するということで、おすすめの順に紹介していました。
改訂版のこの記事では、少ない参考書に絞って紹介していきます!
参考書と過去問は絶対にセットです!
数学検定1級は試験なので過去問の正解率がそのまま合格率になります。
受験数学でも参考書のルートは大事です。
数学検定1級でもこの参考書をやらないと門前払いという参考書はあります。
例えばこの問題をご覧ください。
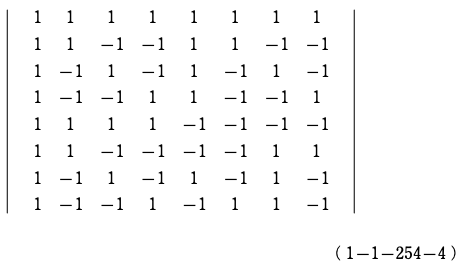
この問題はテクニックを用いて大幅に時間を短縮した上で解答をします。
このような問題のテクニックを知らないのは大きなディスアドバンテージです。
この2冊は内容の被りもなく、過去問を中心とした構成となっております。
本書が理解できないと数学検定1級の合格は無理だと思うくらいのオススメ参考書です!
到達点はどのような感じですか?
1次試験のパターンはこれで合格するくらいには網羅できます。
2次試験は運が良ければこの2冊で合格点までカバーできます。
2次についてはどのような補強をすればいいですか?
受験数学の典型問題の確認+大学数学の底力をカバーしましょう!
受験数学の知識が東大とは言わないまでも、ある程度はないとその時点で数学検定1級は無謀です。
受験数学の参考書についてはこちらの制覇が完了の目安になります。
本書のレベルは受験数学の典型問題(青チャートの例題よりワンランク上)を少ない問題で攻略していく本です。
いろんな解き方があるので、数学的な底力がつきます。
『やさ理』が難しくて読めない人はご自身に合った本を検索してみましょう!
2次の応用数学部分は『マセマ』シリーズを軸に対策を進めるのがおすすめです。
マセマシリーズを読み込みましょう!種類が豊富なので記事の最後に必須のものを最後に紹介します。
高校生の時にその作戦で受かっているから、試してみる価値はありそうですね!
大学院入試を目指している方なら、大学院数学の問題を俯瞰できる本がおすすめですが、東大院や京大院などの最難関の問題があまり載っていない本がおすすめです!
2次の合格力を目指すなら、最近の問題に多く触れることが大切です。
他にも過去問が載っている本はありますが、効率的な面を考慮すると、本書が難易度的にも高めでおすすめできます。
数学検定1級合格体験記

合格するまで3回受験をしました。
初挑戦は高校2年生の秋でした。1次がボロボロで1.5点でした。あと3.5点足りませんでした。
しかしこのまま終われないと思い2次試験でくらいつきました。
結果は2次のみ合格しました。
高校3年生の春に2回目の挑戦をしました。
この時は3.5点で合格点まで1完半足りませんでした。
最後の挑戦は高校3年生の夏でした。
当時は情報が全くなかったので大学数学の本を読み込んで、受験会場のお台場へ向かいました。
何か1つでも高校時代に成し遂げたい。
数学検定1級に絶対に合格したい。
結果は5.0点でギリギリ合格でした。
数学検定1級に合格して数学が好きになりました。
数学は積み重ねの学問です。1つ1つクリアしていけば目的地にたどり着くことができます。
数学検定1級は努力をすれば合格できます。頑張るチャレンジャーを僕はずっと応援しています。









